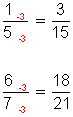Clase 15 de Marzo

Objetivo(s) de la Clase:

·          Resolver problemas cotidianos que involucren cálculos con números superiores o iguales a seis cifras


El agua y los números: lee atentamente y luego responde las preguntas 1, 2 y 3.


El agua es el elemento más importante para la vida en este planeta. Es probable que sin el agua nunca hubiera surgido la vida.

 Se cree que el agua fue traída en parte por meteoritos cuando el planeta estaba en formación.

 

Desde entonces, casi todos los seres vivos han necesitado el agua para sobrevivir. Pero recién hasta el siglo pasado no teníamos agua pura,  cómo la que tienes ahora cuando abres una llave de tu baño o cocina.

 

Hoy en  día  existen plantas procesadoras de  agua  que  se dedican a producir agua de mucha pureza. Esta es el agua cristalina que bebes y que por lo mismo se denomina agua potable. Por ejemplo, en Santiago se producen aproximadamente un  millón  trescientos  veinte  mil  litros  de agua potable por minuto y en Rancagua se producen aproximadamente 37.450 litros por minuto.
  1.  ¿Cuánta agua se produce aproximadamente en Santiago?

 

a)  1.320 litros
b)   13.200 litros
c)   132.000 litros
d)  1.320.000 litros

 

2.  ¿Cuánta agua se produce aproximadamente en Rancagua?

a)  Treinta millones cuatrocientos cincuenta litros.
b)  Treinta y siete mil cuatrocientos cincuenta litros.
c)  Treinta y siete cuatrocientos cincuenta litros.
d)  Treinta y siete mil cuatrocientos litros.

3.  ¿Dónde se produce más agua?

a)  En Santiago
b)  En ambas ciudades
c)  En Chile
d)  En Rancagua



  

I UNIDAD: Numeros Enteros y Decimales"

PRIMERA UNIDAD: "NUMEROS ENTEROS Y DECIMALES"

1.- Lectura y Escritura de Números

La lectura y escritura de números se caracteriza por la forma en la que se colocan las cifras y se leen de acuerdo a su posición.

Para leer o escribir números de cualquier cantidad es conveniente separarlos en grupos de tres dígitos de esta forma tu podrás escribir y leer cualquier cifra ya sea muy grande o muy pequeña.

y se lee:
- Cinco Unidades (5)
- Una Decena y 0 Unidades (10)
- Una Centena, 0 Decenas y 0 Unidades (100)

Completa la tabla, siguiendo la secuencia dada.

PROGRAMA DE CONTENIDOS 2016

I.- UNIDAD: "NÚMEROS ENTEROS Y DECIMALES"

1.- Valor Posicional hasta los mil Millones.
a.- Comparar y Ordenar Números Enteros
b.- Redondear números enteros
c.- Estimar sumas y Diferencias
d.- Sumar y Restar Números Enteros
e.- Calculo Mental: Suma y Resta
f.- Algebra Expresiones de Sumas y Restas
g.- Resolución de Problemas: Estrategia: buscar patrón.

2.- Multiplicar números enteros
a.- Calculo mental: Patrones en los múltiplos
b.- Estimar productos.
c.- Propiedad Distributiva.
d.- Multiplicar por números de 1 dígito.
e.- Multiplicar por  números de 2 dígitos.
f.- Resolución de Problemas, Estrategia predecir y probar.

3.- Dividir entre divisores de 1 y 2 dígitos:
a.- Estimar con divisores de 1 digito
b.- Dividir entre divisores de 1 dígito
c.- Algebra Patrones de División.
d.- Dividir con residuos o restos.
e.- Resolución de Problemas, Destreza: Interpretar el resto.
f.- Dividir Números de 3 dígitos por números de 1 digito.
g.- Cero en la División.

4.- Álgebra: Usar las operaciones de Multiplicación y División.
a.- Propiedad de la Multiplicación.
b.- Prevalencia de las Operaciones.
c.- Expresiones entre paréntesis.
d.- Escribir y evaluar expresiones.
e) Patrones: Hallar una Regla.

II.- UNIDAD: "NUMEROS Y CONCEPTO DE FRACCIONES"
1.- Concepto de Fracciones
a.- Fracciones equivalentes.
b.- Fracciones irreductibles.
c.- Números Mixtos
d.- Comparar y ordenar fracciones y números mixtos.
e.- Resolución de Problemas, Estrategia: hacer un modelo.
f.- Relacionar Fracciones y Decimales.
g.- Usar una recta numérica.

2.- Sumar y Restar fracciones semejantes.
a.- Representar la suma y la resta.
b.- Sumar y restar fracciones semejantes.
c.- Sumar y restar números mixtos semejantes
d.- Restar haciendo conversiones
e.- Resolución de Problemas, Estrategia trabajar desde el final hasta el principio.

3.- Sumar y Restar fracciones no semejantes.
a.- Representar la suma de fracciones no semejantes
b.- Representar la resta de fracciones no semejantes.
c.- Estimar sumas y diferencias.
d.- Usar denominadores Comunes
e.- Sumar y Restar Fracciones
f.- Resolución de problemas.

III.- UNIDAD: "OPERACIONES DECIMALES"



IV.- UNIDAD: "GEOMETRIA Y MEDICION"



V.- UNIDAD "DATOS Y GRAFICOS"
                                                                         

BIENVENIDOS AL MUNDO DE LAS MATEMATICAS DE 5° AÑO DE E.G.B.

El objetivo de este cuaderno de matemáticas digital, es poner al alcance de los alumnos y  apoderados de Quinto Año, de la Escuela Emilia Lascar de Peñaflor, los contenidos de la asignatura, con el fin de que los repasen y/o se pongan al día de las materias tratadas en clases.

Sin duda, para los Señores Padres, esta herramienta será de gran ayuda, para saber lo que están aprendiendo sus hijos, y así ayudarlos a estudiar. No olvidemos, que los primeros educadores son los padres, y para los niños resulta muy gratificante ver y sentir que sus padres se interesan por sus logros y aprendizajes, que les servirán para su vida, y llegar a ser grandes personas, al servicio de ellos mismos, de su entorno y de la sociedad toda.

Los invitamos a conocer este sencillo blog, y a adentrarse al fabuloso mundo de las matemáticas, y recuerden... ¡QUERER ES PODER!

Atte

      Mario Barrera García
          Profesor de E.G.B.
Postitulo en Informática Educativa

UNIDAD 5ta. "GEOMETRIA"

Contenidos de la Unidad:

1.- Clasificación de los Angulos.
2.- Medición de los Angulos.
3.- Unidades de Medida de Longitud y de Superficie.
4.- Perimetro de Triángulos.
5.- Perimetro de Cuadrados y Rectangulos.
6.- Perimetros y Areas de Cudrados y Rectanglos
7.- Areas de Triangulos
8.- Areas de Figuras Compuestas.
9.- Variaciones de Perimetros y Areas

1.- CLASIFICACION DE LOS ANGULOS



2..- MEDICION DE ANGULOS


3.- UNIDADES DE MEDIDA DE LONGITUD Y DE SUPERFICIE

El sistema métrico decimal, también llamado sistema métrico, es un conjunto de patrones
 de medida que permiten comparar lo que se desea medir con una unidad básica, En este sistema hay unidades de Longitud, Superficie y masa, entre otras.

La unidad de medida universal que se utiliza para las longitudes es el metro (m), pero existen múltiplos que son el Kilómetro (km), Hectómetro (hm) y Decámetro (dam), los que se usan para expresar longitudes más grandes; y los submúltiplos, como el Decímetro (dm), centimétro (cm) y el milímetro (mm), que usamos para medir longitudes más pequeñas.

La unidad de medida universal que se utiliza para las superficies es el metro cuadrado.
Sus múltiplos son: Kilómetro Cuadrado, Hectómetro Cuadrado y Decámetro Cuadrado.
Submúltiplos son; Decímetro Cuadrado, Centímetro Cuadrado y Milímetro Cuadrado.

4.- PERÍMETROS DE TRÍANGULOS

El perímetro de una figura es la medida total de su frontera o contorno, expresada en la misma unidad de longitud. Lo simbolizamos con la letra P.

Para expresar el perímetro de figuras pequeñas utilizamos generalmente el milímetro o el centímetro; cuando son figuras  más grandes (como el ancho de una Pared) utilizamos el metro y cuando son más grandes aún, como son las distancias entre dos ciudades, utilizamos el kilómetro.

Para calcular el Perímetro de Tríangulos solametente debemos sumar la longitud de sus lados.

5.- PERIMETRO DE CUADRADOS Y RECTANGULOS



Los lados del rectángulo de la figura miden 10 cm. y 5 cm.

10 cm

10 cm

El perímetro del rectángulo lo obtenemos sumando todos sus lados:

Perímetro = 10 cm + 5 cm + 10 cm + 5 cm = 30 cm

Por lo tanto, el perímetro del rectángulo es 30 cm.

Respecto al cuadrado, el perímetro (la longitud de su contorno) se obtiene sumando sus cuatro lados.


6.-  PERIMETRO Y AREA DE CUADRADOS Y RECTANGULOS

El área es la medida de la superficie de una figura.

Para expresar el área de superficies pequeñas utilizamos generalmente el milímetro cuadrado o el centímetro cuadrado; cuando son superficies más grandes  (como la de una Pared) utilizamos el metro cuadrado y cuando son más grandes aún (como la de una ciudad) utilizamos el Kilómetro cuadrado.

* El área de un cuadrado de lado a es igual al producto de la medida de su lado por si mismo, es decir:
                                          A = a x a

* El área de un rectángulo de lados a y b es igual al producto de la medida de su largo por su ancho.

                                          A = a x b

Área: es la medida de la superficie de una figura; es decir, la medida de su región interior.

Área de un rectángulo

El área del rectángulo corresponde a la medida de la región verde, y se obtiene multiplicando la base por la altura.

Área = base · altura

Ejemplo:

Los lados del rectángulo de la figura miden 10 cm. y 5 cm.

10 cm	La altura de este rectángulo mide 5 cm.
10 cm	La base de este rectángulo mide 10 cm.

Área = 10 · 5 = 50 cm2

el área del rectángulo es 50 cm²

El centímetro cuadrado (cm2) es una unidad que nos permite medir áreas. También pueden ser metros cuadrados (m2), milímetros cuadrados (mm2), etc.

Área del cuadrado

El área de un cuadrado es igual al producto de lado por lado.

7.- AREA DEL TRIANGULO


Calculemos el Área del siguiente triángulo

Reemplazando los datos de la formula obtenemos:





8.- AREA DE FIGURAS COMPUESTAS:

CONTENIDOS DE LA 4ta. UNIDAD "DECIMALES"

1.- LECTURA Y ESCRITURA DE DECIMALES

Un número con decimales se lee nombrando primero la parte entera seguida de la palabra unidades y luego la parte decimal citando las unidades que representa la ultima cifra de la derecha:
15,364 = 15 unidades 364 milésimas.

Se escribe anotando primero la parte entera seguida de una coma y poniendo a continuación la parte decimal haciendo coincidir la ultima cifra con las unidades citadas:
5 unidades 20 milésimas = 5,020.
Si falta alguna clase de unidades, se pone cero en su lugar

PINCHA AQUI, PARA REALIZAR EJERCICIO

Actividad: Pàgina 106 y 107 del texto del alumno

Ver Video

2,- RELACION ENTRE FRACCIONES Y DECIMALES

Visite el siguiente Enlace

UNIDAD 4: DECIMALES

CONTENIDOS DE LA UNIDAD

1.- Lectura y escritura de decimales

2.- Relaciòn entre Decimales y Fracciones

3.- Decimales, Fracciones y Nùmeros Naturales en la Recta Numérica.

4.- Orden y Comparación

5.- Adición y Sustracción de nùmeros decimales


METODO DE TRABAJO

a) Desarrollo de Guías

b) Ejercicios en Clases

c) Ejercicios On Line.

d) Prueba Escrita.

RESULTADOS Y CORRECCION DE PRUEBAS

QUINTO AÑO  "A"

QUINTO AÑO  "B"

QUINTO AÑO  "C"

Publicaremos la corrección de prueba aplicada hoy jueves.-

OPERACIONES DE FRACCIONES COMBINADAS

1) Simplificar Fracciones;

Las fracciones pueden tener numeradores y denominadores que son números compuestos (números que tienen otros factores además de 1 y el número mismo).

Como simplificar una fracción:

• Encuentra un común divisor del numerador y del denominador. Un divisor común es un número que se puede dividir en forma exacta por los dos números. Dos es un divisor común de 4 y 14.
• Divide ambos el numerador y el denominador por el divisor común.
• Repite este proceso hasta que no haya más divisores comunes.
• La fracción se simplifica cuando no hay más divisores comunes.

Otro método para simplificar una fracción.

• Encuentra el Máximo Común Divisor (MCD) del numerador y del denominador.
• Divide el numerador y el denominador por el MCD.

2) Amplificar Fracciones:

Es multiplicar el denominador y numerador de una fracción por un mismo número. Este número permite que la fracción aumente de valor tantas veces como veces se amplifica.

Por ejemplo, si la fracción se amplifica por dos, significa que aumentará su valor al doble.

Siempre que se amplifique una fracción se obtendrán fracciones equivalentes; es decir, fracciones que representan la misma cantidad.

Ejemplos:

Fracciones amplificadas por 3.

3) Encontrar el Máximo Común Divisor (MCD)

El máximo común divisor (m.c.d.) de dos o más números es el mayor de los

divisores comunes.

• Para hallar el máximo común divisor de dos o más números, por ejemplo,

m.c.d. (12, 18), se siguen estos pasos:

1.° Se descompone cada número en producto de factores primos.

12 : 2                      18  : 2
 6  : 2                       9   : 3
 3  : 3                       3   : 3
 1                              1


2.° El producto de estos factores comunes elevados al menor exponente es el máximo común divisor de los números dados.


           2 
12 = 2  x  3

                  2
18 = 2  x  3                                     m.c.d. (12, 18) = 2 x 3 = 6


Practica el MCD

Ver video

Ver 2° Video

GUIA DE EJERCICIOS PARA LA TERCERA UNIDAD "FRACCIONES"

1) Primera Parte: Ingresa Aquì y responde en tu cuaderno.-

A Continuación copia en tu cuadero los siguientes ejercicios y resuelve.

2)  Asociar cada fracción de hora con los minutos correspondientes:

3) Halla los pares de fracciones equivalentes y colócalas en parejas:

4) Escribe los inversos de:

5) Escribe el signo > o <, donde corresponda.

6) Compara las siguientes fracciones:

7)  Ordenar de menor o mayor:

8)  Clasifica las siguientes fracciones en propias o impropias:

9) Calcula las siguientes sumas de fracciones.

12         4         20

+           +           =

7          7          7

                
                   15   +   10   +  21

           11        11        11       =

                    21        14        10

                            +           +           =

                    13        13        13                                                                    

                                                                                               

                    

                      31        41        38

                             +          +           =

                      17        17        17

 10)  Calcula las siguientes restas de fracciones.

  23        14

  -           =

   7          7                                                                  


  43        29

          -           =

   11        11

                       89        78

     -           =

    13        13                                                                  


    103       94

                        -           =

                19        19

11.- Calcula las siguientes sumas de fracciones de distinto denominador:

1          4          1

+           +          =

5          3          2

2          1          3

+           +          =

3          9          5

4          2          1

+           +          =

7          4          8

3          1          1

+           +          =

2          5         10

3          1          3

+           +          =

8          4         16

    12.- Calcula las siguientes restas de fracciones con distinto denominador

4          1                                                              2           4

-           =                                                               -           =

5          7                                                              3           7

3          1

-           =

10        12                                                               9          3

                                                                                               -          =

                                                                                              15         8