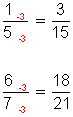1.- Clasificación de los Angulos.
2.- Medición de los Angulos.
3.- Unidades de Medida de Longitud y de Superficie.
4.- Perimetro de Triángulos.
5.- Perimetro de Cuadrados y Rectangulos.
6.- Perimetros y Areas de Cudrados y Rectanglos
7.- Areas de Triangulos
8.- Areas de Figuras Compuestas.
9.- Variaciones de Perimetros y Areas
1.- CLASIFICACION DE LOS ANGULOS
2..- MEDICION DE ANGULOS
3.- UNIDADES DE MEDIDA DE LONGITUD Y DE SUPERFICIE
El sistema métrico decimal, también llamado sistema métrico, es un conjunto de patrones
de medida que permiten comparar lo que se desea medir con una unidad básica, En este sistema hay unidades de Longitud, Superficie y masa, entre otras.
La unidad de medida universal que se utiliza para las longitudes es el metro (m), pero existen múltiplos que son el Kilómetro (km), Hectómetro (hm) y Decámetro (dam), los que se usan para expresar longitudes más grandes; y los submúltiplos, como el Decímetro (dm), centimétro (cm) y el milímetro (mm), que usamos para medir longitudes más pequeñas.
La unidad de medida universal que se utiliza para las superficies es el metro cuadrado.
Sus múltiplos son: Kilómetro Cuadrado, Hectómetro Cuadrado y Decámetro Cuadrado.
Submúltiplos son; Decímetro Cuadrado, Centímetro Cuadrado y Milímetro Cuadrado.
4.- PERÍMETROS DE TRÍANGULOS
El perímetro de una figura es la medida total de su frontera o contorno, expresada en la misma unidad de longitud. Lo simbolizamos con la letra P.
Para expresar el perímetro de figuras pequeñas utilizamos generalmente el milímetro o el centímetro; cuando son figuras más grandes (como el ancho de una Pared) utilizamos el metro y cuando son más grandes aún, como son las distancias entre dos ciudades, utilizamos el kilómetro.
Para calcular el Perímetro de Tríangulos solametente debemos sumar la longitud de sus lados.
5.- PERIMETRO DE CUADRADOS Y RECTANGULOS
Los lados del rectángulo de la figura miden 10 cm. y 5 cm.
10 cm
|
 |
10 cm
|
El perímetro del rectángulo lo obtenemos sumando todos sus lados:
Perímetro = 10 cm + 5 cm + 10 cm + 5 cm = 30 cm
|
Por lo tanto, el perímetro del rectángulo es 30 cm.
Respecto al cuadrado, el perímetro (la longitud de su contorno) se obtiene sumando sus cuatro lados.
6.- PERIMETRO Y AREA DE CUADRADOS Y RECTANGULOS
El área es la medida de la superficie de una figura.
Para expresar el área de superficies pequeñas utilizamos generalmente el milímetro cuadrado o el centímetro cuadrado; cuando son superficies más grandes (como la de una Pared) utilizamos el metro cuadrado y cuando son más grandes aún (como la de una ciudad) utilizamos el Kilómetro cuadrado.
* El área de un cuadrado de lado a es igual al producto de la medida de su lado por si mismo, es decir:
A = a x a
* El área de un rectángulo de lados a y b es igual al producto de la medida de su largo por su ancho.
A = a x b
6.- PERIMETRO Y AREA DE CUADRADOS Y RECTANGULOS
El área es la medida de la superficie de una figura.
Para expresar el área de superficies pequeñas utilizamos generalmente el milímetro cuadrado o el centímetro cuadrado; cuando son superficies más grandes (como la de una Pared) utilizamos el metro cuadrado y cuando son más grandes aún (como la de una ciudad) utilizamos el Kilómetro cuadrado.
* El área de un cuadrado de lado a es igual al producto de la medida de su lado por si mismo, es decir:
A = a x a
* El área de un rectángulo de lados a y b es igual al producto de la medida de su largo por su ancho.
A = a x b
Área: es la medida de la superficie de una figura; es decir, la medida de su región interior.
Área de un rectángulo
 |
El área del rectángulo corresponde a la medida de la región verde, y se obtiene multiplicando la base por la altura.
Área = base · altura
|
Ejemplo:
Los lados del rectángulo de la figura miden 10 cm. y 5 cm.
10 cm
| La altura de este rectángulo mide 5 cm. |
 | |
10 cm
| La base de este rectángulo mide 10 cm. |
Área = 10 · 5 = 50 cm2
|
el área del rectángulo es 50 cm2
El centímetro cuadrado (cm2) es una unidad que nos permite medir áreas. También pueden ser metros cuadrados (m2), milímetros cuadrados (mm2), etc.
|
Área del cuadrado
El área de un cuadrado es igual al producto de lado por lado.
7.- AREA DEL TRIANGULO

Calculemos el Área del siguiente triángulo


Calculemos el Área del siguiente triángulo

Reemplazando los datos de la formula obtenemos:

8.- AREA DE FIGURAS COMPUESTAS: